Series & Parallel Circuits — Analysis & Practical Examples

1. Introduction

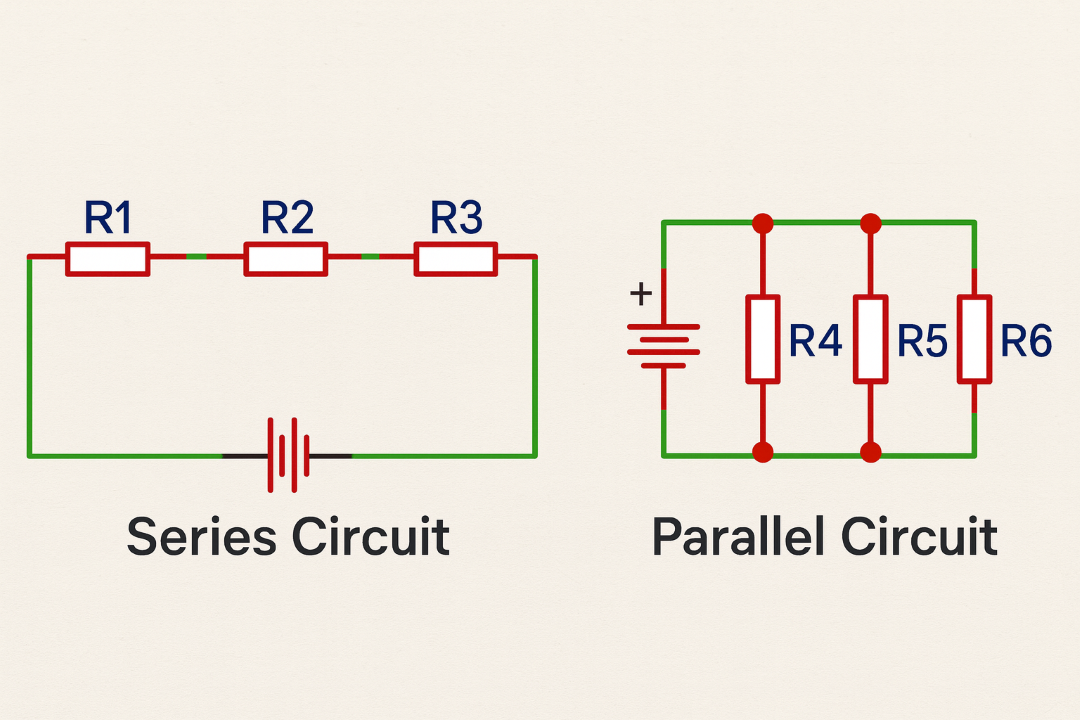
Electrical circuits are typically formed by combining components (resistors, capacitors, inductors, sources) in two fundamental topologies: series and parallel. Understanding the characteristics of each topology enables you to analyze circuits, compute equivalent resistance, voltage drops and current distribution — essential tasks for design and troubleshooting.

2. Series Circuits

In a series circuit, components are connected end-to-end so that the same current flows through every element (I_total = I1 = I2 = …). The supply voltage is divided among the resistances proportionally to their values.

Equivalent resistance

R_total = R1 + R2 + R3 + ...

Voltage drop across a resistor

Since the same current I flows through each resistor:

V_k = I × R_k

Example

With a 12 V source and resistors R1 = 100 Ω, R2 = 200 Ω in series:

R_total = 100 + 200 = 300 Ω
I = V / R_total = 12 / 300 = 0.04 A (40 mA)
V_R1 = I × R1 = 4 V
V_R2 = I × R2 = 8 V

3. Parallel Circuits

In a parallel circuit, elements are connected across the same two nodes; therefore, the voltage across each branch is equal (V_total = V1 = V2 = …). The total current is the sum of branch currents.

Equivalent resistance

1 / R_total = 1 / R1 + 1 / R2 + 1 / R3 + ...
For two resistors:
R_eq = (R1 × R2) / (R1 + R2)

Current division

I1 = V / R1
I2 = V / R2
I_total = I1 + I2

Example

A 10 V source feeds two parallel resistors R1 = 100 Ω and R2 = 200 Ω:

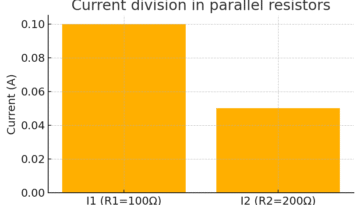
I1 = 10 / 100 = 0.10 A
I2 = 10 / 200 = 0.05 A
I_total = 0.15 A
R_eq = 1 / (1/100 + 1/200) = 66.67 Ω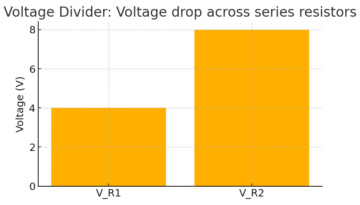

4. Quick calculation tips

• Add resistances for series connections.
• Use reciprocal formula for parallel networks; for convenience, reduce pairwise.
• For mixed series-parallel networks, reduce sub-networks step by step to a single equivalent.

5. Practical applications

The voltage divider is a common use of series resistors — it creates a scaled voltage reference for sensors, ADC inputs, or bias networks:

V_out = V_in × (R2 / (R1 + R2))  

Example: V_in = 12 V, R1 = 1 kΩ, R2 = 2 kΩ → V_out = 8 V.

6. Practice problems

Problem 1: Compute the total resistance for this network: R1 = 220 Ω in parallel with the series pair (R2 = 330 Ω + R3 = 470 Ω). (Hint: compute R2 + R3 first, then parallel with R1.)

Problem 2: Design a divider to produce 3.3 V from a 12 V source to feed a sensor drawing ~5 mA. Choose R1 and R2 so that the divider’s output impedance is low enough (e.g., divider impedance ≤ 1/10 of sensor input impedance).

7. Practical notes

• Always verify power dissipation (P = I²R or P = V²/R) across resistors to avoid overheating.
• When using a voltage divider for low-impedance loads, include a buffer (op-amp follower) to prevent loading errors.
• Simulate circuits with LTspice, Falstad, or Proteus before building physical prototypes.

8. Conclusion

Mastering series and parallel analysis is fundamental for circuit design and troubleshooting. The ability to reduce complex networks into simpler equivalents makes solving real-world electrical problems manageable and reliable.

References

• Paul Horowitz & Winfield Hill, The Art of Electronics, 3rd Edition, Cambridge University Press, 2015.
• Thomas L. Floyd, Electronics Fundamentals, Pearson.

Keywords: series circuit, parallel circuit, equivalent resistance, voltage divider, current division, basic electronics